
Mecânica quântica
A Mecânica Quântica é o estudo dos sistemas físicos cujas dimensões são próximas ou abaixo da escala atômica, tais como moléculas, átomos, elétrons, prótons e de outras partículas subatômicas. A Mecânica Quântica é um ramo fundamental da física com vasta aplicação. A teoria quântica generaliza a mecânica clássica e fornece descrições exatas para muitos fenômenos previamente inexplicados tais como a radiação de corpo negro e as órbitas estáveis do elétron. Os efeitos específicos da mecânica quântica não são somente perceptíveis em escalas microscópicas. Por exemplo, a explicação de fenômenos macroscópicos como a super fluidez e a supercondutividade só é possível se considerarmos que o comportamento microscópico da matéria é quântico.
A mecânica quântica recebe esse nome por prever um fenômeno bastante conhecido dos físicos: a quantização. No caso dos estados ligados (por exemplo, um elétron orbitando em torno de um núcleo positivo) a Mecânica Quântica prevê que a energia (do elétron) deve ser quantizada. Este fenômeno é completamente alheio ao que prevê a teoria clássica.
Um Panorama Geral
A palavra “quântica” (do Latim, quantum) quer dizer quantidade. Na mecânica quântica, esta palavra refere-se a uma unidade discreta que a teoria quântica atribui a certas quantidades físicas, como a energia de um elétron ligado a um átomo em repouso. A descoberta de que as ondas eletromagnéticas podem ser explicadas como uma emissão de pacotes de energia (chamados quanta) conduziu ao ramo da física que lida com sistemas atômicos e subatômicos. Este ramo da física é chamado hoje mecânica quântica.
A mecânica quântica é a base teórica e experimental de vários campos da Física e da Química, incluindo a física da matéria condensada, física do estado sólido, física atômica, física molecular, química computacional, química quântica, física de partículas, e física nuclear. Os alicerces da mecânica quântica foram estabelecidos durante a primeira metade do século XX por Albert Einstein, Werner Heisenberg, Max Planck, Louis de Broglie, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, Richard Feynman e outros. Alguns aspectos fundamentais da contribuição desses autores ainda são alvo de investigação.
Normalmente é necessário utilizar a mecânica quântica para compreender o comportamento de sistemas em escala atômica. Por exemplo, se a mecânica clássica governasse o funcionamento de um átomo, o modelo planetário do átomo – proposto pela primeira vez por Rutherford – seria um modelo completamente instável. Segundo a teoria eletromagnética clássica, toda a carga elétrica acelerada emite radiação. Por outro lado, o processo de emissão de radiação consome a energia da partícula. Dessa forma, o elétron, enquanto caminha na sua órbita, perderia energia continuamente até colapsar contra o núcleo positivo! Com efeito, o modelo planetário do átomo é um modelo ineficaz. Para explicar o comportamento de um elétron em torno de um átomo de hidrogênio é necessário utilizar as leis da mecânica quântica.
O Conceito de Estado na Mecânica Quântica
Em física, chama-se sistema um fragmento concreto da realidade que foi separado para estudo. Dependendo do caso, a palavra sistema refere-se a um elétron ou um próton, um pequeno átomo de hidrogênio ou um grande átomo de urânio, uma molécula isolada ou um conjunto de moléculas interagentes formando um sólido ou um vapor. Em todos os casos, sistema é um fragmento da realidade concreta para o qual deseja-se chamar atenção.
Os sistemas físicos não são estáticos, eles evoluem. Essa idéia conduz a outro conceito-chave, que tem especial importância na física quântica: o conceito de estado.
Cada sistema ocupa um estado num instante no tempo e as leis da física devem ser capazes de descrever como um dado sistema parte de um estado e chega a outro. Em outras palavras, as leis da física devem dizer como o sistema evolui (de estado em estado).
No estudo da mecânica quântica, é usual ressaltar que todas as informações possíveis de se conhecer em um dado sistema constituem seu estado. Essa definição pode parecer simples e evidente, mas ela esconde um cuidado sutil e muito importante.
Muitas variáveis que ficam bem determinadas na mecânica clássica são substituídas por distribuições de probabilidades na mecânica quântica, gerando algum desconforto inicial no estudante que já está acostumado a pensar classicamente.
Muitas vezes não é possível saber com exatidão algumas informações óbvias sobre as partículas - como sua posição, por exemplo. Como o estado é caracterizado pelas informações que podemos conhecer, sendo impossível saber de antemão a posição de uma partícula, dizemos que essa informação não constitui seu estado. Graças a essa definição sutil de estado físico, o eventual desconhecimento de alguma grandeza não é um problema (pelo menos na mecânica quântica).
Em todo o caso, seguimos calculando.
A representação do estado
No formalismo da mecânica quântica, o estado de um sistema num dado instante de tempo pode ser representado de duas formas principais: (1) O estado é representado por uma função complexa das posições ou dos momenta de cada partícula que compõe o sistema. Essa representação é chamada função de onda. (2) Também é possível representar o estado por um vetor num espaço vetorial complexo. Esta representação do estado quântico é chamada vetor de estado. Devido à notação introduzida por Paul Dirac, tais vetores são usualmente chamados kets (sing.: ket).
Em suma, tanto as funções de onda quanto os vetores de estado (ou kets) representam os estados de um dado sistema físico de forma completa e equivalente e as leis da mecânica quântica descrevem como vetores de estado e funções de onda evoluem no tempo.
Estes objetos matemáticos abstratos (kets e funções de onda) permitem o cálculo da probabilidade de se obter resultados específicos em um experimento concreto. Por exemplo, o formalismo da mecânica quântica permite que se calcule a probabilidade de encontrar um elétron em uma região particular em torno do núcleo.
Para compreender seriamente o cálculo das probabilidades a partir da informação representada nos vetores de estado e funções de onda é preciso dominar alguns fundamentos de álgebra linear.
Primeiros Fundamentos Matemáticos
É impossível falar seriamente sobre mecânica quântica sem fazer alguns apontamentos matemáticos. Isso porque muitos fenômenos quânticos difíceis de se imaginar concretamente podem ser representados sem mais complicações com um pouco de abstração matemática.
Há três conceitos fundamentais da matemática - mais especificamente da álgebra linear - que são empregados constantemente pela mecânica quântica. São estes: (1) o conceito de operador; (2) de autovetor; e (3) de autovalor.
Vetores e Espaços Vetoriais
Na álgebra linear, um espaço vetorial (ou o espaço linear) é uma coleção dos objetos abstratos (chamados vetores) que possuem algumas propriedades que não serão completamente detalhadas aqui.
Por agora, importa saber que tais objetos (vetores) podem ser adicionados uns aos outros e multiplicados por um número escalar. O resultado dessas operações é sempre um vetor pertencente ao mesmo espaço. Os espaços vetoriais são os objetos básicos do estudo na álgebra linear, e têm várias aplicações na matemática, na ciência, e na engenharia.
O espaço vetorial mais simples e familiar é o espaço Euclidiano bidimensinal. Os vetores neste espaço são pares ordenados e são representados graficamente como "setas" dotadas de módulo, direção e sentido. No caso do espaço euclidiano bidimensional, a soma de dois vetores quaisquer pode ser realizada utilizando a regra do paralelogramo.
Todos os vetores também podem ser multiplicados por um escalar - que no espaço Euclidiano é sempre um número real. Esta multiplicação por escalar poderá alterar o módulo do vetor e seu sentido, mas preservará sua direção. O comportamento de vetores geométricos sob estas operações fornece um bom modelo intuitivo para o comportamento dos vetores em espaços mais abstratos, que não precisam de ter a mesma interpretação geométrica. Como exemplo, é possível citar o espaço de Hilbert (onde "habitam" os vetores da mecânica quântica). Sendo ele também um espaço vetorial, é certo que possui propriedades análogas àquelas do espaço Euclidiano.
Os operadores na mecânica quântica
Um operador é um ente matemático que estabelece uma relação funcional entre dois espaços vetoriais. A relação funcional que um operador estabelece pode ser chamada transformação linear. Os detalhes mais formais não serão apontados aqui. Interessa, por enquanto, desenvolver uma idéia mais intuitiva do que são esses operadores.
Por exemplo, considere o Espaço Euclidiano. Para cada vetor nesse espaço é possível executar uma rotação (de um certo ângulo) e encontrar outro vetor no mesmo espaço. Como essa rotação é uma relação funcional entre os vetores de um espaço, podemos definir um operador que realize essa transformação. Assim, dois exemplos bastante concretos de operadores são os de rotação e translação.
Do ponto de vista teórico, a semente da ruptura entre as física quântica e clássica está no emprego dos operadores. Na mecânica clássica, é usual descrever o movimento de uma partícula com uma função escalar do tempo. Por exemplo, imagine que vemos um vaso de flor caindo de uma janela. Em cada instante de tempo podemos calcular a que altura se encontra o vaso. Em outras palavras, descrevemos a grandeza posição com um número (escalar) que varia em função do tempo.
Uma característica distintiva na mecânica quântica é o uso de operadores para representar grandezas físicas. Ou seja, não são somente as rotações e translações que podem ser representadas por operadores. Na mecânica quântica grandezas como posição, momento linear, momento angular e energia também são representados por operadores.
Até este ponto já é possível perceber que a mecânica quântica descreve a natureza de forma bastante abstrata. Em suma, os estados que um sistema físico pode ocupar são representados por vetores de estado (kets) ou funções de onda (que também são vetores, só que no espaço das funções). As grandezas físicas não são representadas diretamente por escalares (como 10 m, por exemplo), mas por operadores.
Para compreender como essa forma abstrata de representar a natureza fornece informações sobre experimentos reais é preciso discutir um último tópico da álgebra linear: o problema de autovalor e autovetor.
O Problema de Autovalor e Autovetor
O problema de autovalor e autovetor é um problema matemático abstrato sem o qual não é possível compreender seriamente o significado da mecânica quântica.
Em primeiro lugar, considere o operador  de uma transformação linear arbitrária que relacione vetores de um espaço E com vetores do mesmo espaço E. Neste caso, escreve-se [eq.01]:
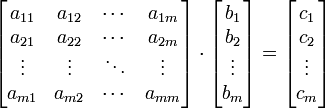
Observe que qualquer matriz quadrada satisfaz a condição imposta acima desde que os vetores no espaço E possam ser representados como matrizes-coluna e que a atuação de  sobre os vetores de E ocorra conforme o produto de matrizes a seguir:
Como foi dito, a equação acima ilustra muito bem a atuação de um operador do tipo definido em [eq.01]. Porém, é possível representar a mesma idéia de forma mais compacta e geral sem fazer referência à representação matricial dos operadores lineares [eq.02]:
Para cada operador  existe um conjunto  tal que cada vetor do conjunto satisfaz [eq.03]:
tal que cada vetor do conjunto satisfaz [eq.03]:
A equação acima é chamada equação de autovalor e autovetor. Os vetores do conjunto  são chamados autovetores. Os escalares do conjunto
são chamados autovetores. Os escalares do conjunto  são chamados autovalores. O conjunto dos autovalores λi também é chamado espectro do operador Â.
são chamados autovalores. O conjunto dos autovalores λi também é chamado espectro do operador Â.
Para cada autovalor corresponde um autovetor e o número de pares autovalor-autovetor é igual à dimensão do espaço E onde o operador  está definido. Em geral, o espectro de um operador  qualquer não é contínuo, mas discreto. Encontrar os autovetores e autovalores para um dado operador  é o chamado problema de autovalor e autovetor.
De antemão o problema de autovalor e autovetor possui duas características:
(1)  satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo
satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo  não é considerado uma resposta do problema.
não é considerado uma resposta do problema.
(2) Se  satisfaz a equação de autovalor e autovetor, então seu múltiplo
satisfaz a equação de autovalor e autovetor, então seu múltiplo 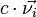 também é uma resposta ao problema para qualquer
também é uma resposta ao problema para qualquer  .
.
Enfim, a solução geral do problema de autovalor e autovetor é bastante simples. A saber:
Onde:
Como  não pode ser considerado uma solução do problema, é necessário que:
não pode ser considerado uma solução do problema, é necessário que:
A equação acima é um polinômio de grau n. Portanto, para qualquer operador  há n quantidades escalares
há n quantidades escalares 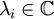 distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
Os autovetores correspondentes aos autovalores  de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
[editar] O significado físico dos operadores, seus autovetores e autovalores
Para compreender o significado físico de toda essa representação matemática abstrata, considere o exemplo do operador de Spin na direção z:  .
.
Na mecânica quântica, cada partícula tem associada a si uma quantidade sem análogo clássico chamada spin ou momento angular intrínseco. O spin de uma partícula é representado como um vetor com projeções nos eixos x, y e z. A cada projeção do vetor spin : corresponde um operador:
corresponde um operador:
O operador ![\hat{S_z}]](http://upload.wikimedia.org/math/2/f/c/2fc0171fe3f22a300d71cfe2b8be7571.png) é geralmente representado da seguinte forma:
é geralmente representado da seguinte forma:
É possível resolver o problema de autovetor e autovalor para o operador  . Nesse caso obtem-se:
. Nesse caso obtem-se:
Portanto, os autovalores são:
Aspectos Históricos
A história da mecânica quântica começou essencialmente em 1838 com a descoberta dos raios catódicos por Michael Faraday, a enunciação em 1859 do problema da radiação de corpo negro por Gustavo Kirchhoff, a sugestão 1877 por Ludwig Boltzmann que os estados de energia de um sistema físico poderiam ser discretos, e a hipótese por Planck em 1900 de que toda a energia é irradiada e absorvida na forma de elementos discretos chamados quanta. Segundo Planck, cada um desses quanta tem energia proporcional à frequência ν da radiação eletromagnética emitida ou absorvida.

Princípios da Mecânica Quântica
- Primeiro Princípio: Princípio da superposição
Na mecânica quântica, o estado de um sistema físico é definido pelo conjunto de todas as informações que podem ser extraídas desse sistema ao se efetuar alguma medida.
Na mecânica quântica, todos os estados são representados por vetores em um espaço vetorial complexo: o Espaço de Hilbert H. Assim, cada vetor no espaço H representa um estado que poderia ser ocupado pelo sistema. Portanto, dados dois estados quaisquer, a soma algébrica (superposição) deles também é um estado.
Como a norma (matemática) dos vetores de estado não possui significado físico, todos os vetores de estado são preferencialmente normalizados. Na notação de Dirac, os vetores de estado são chamados "Kets" e são representados como aparece a seguir:
Usualmente, na matemática, são chamados funcionais todas as funções lineares que associam vetores de um espaço vetorial qualquer a um escalar. É sabido que os funcionais dos vetores de um espaço também formam um espaço, que é chamado espaço dual. Na notação de Dirac, os funcionais - elementos do Espaço Dual - são chamados "Bras" e são representados como aparece a seguir:
- Segundo Princípio: medida de grandezas físicas
-
- a) Para toda grandeza física A é associado um operador linear auto-adjunto  pertencente a A:  é o observável (autovalor do operador) representando a grandeza A.
- b) Seja
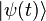 o estado no qual o sistema se encontra no momento onde efetuamos a medida de A. Qualquer que seja
o estado no qual o sistema se encontra no momento onde efetuamos a medida de A. Qualquer que seja 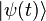 , os únicos resultados possíveis são os autovalores de aα do observável Â.
, os únicos resultados possíveis são os autovalores de aα do observável Â. - c) Sendo
 o projetor sobre o subespaço associado ao valor próprio aα, a probablidade de encontrar o valor aα em uma medida de A é:
o projetor sobre o subespaço associado ao valor próprio aα, a probablidade de encontrar o valor aα em uma medida de A é:  onde
onde 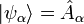
- d) Imediatamente após uma medida de A, que resultou no valor aα, o novo estado
 do sistema é
do sistema é
- Terceiro Princípio: Evolução do sistema
Seja 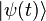 o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
onde  é o hamiltoniano do sistema.
é o hamiltoniano do sistema.
Conclusões da Mecânica Quântica
As conclusões mais importantes desta teoria são:
- Em estados ligados, como o elétron girando ao redor do núcleo de um átomo, a energia não se troca de modo contínuo, mas sim de modo discreto (descontínuo), em transições cujas energias podem ou não ser iguais umas às outras. A idéia de que estados ligados têm níveis de energias discretas é devida a Max Planck.
- O de ser impossível atribuir ao mesmo tempo uma posição e um momentum exatas a uma partícula, renunciando-se assim ao conceito de trajetória, vital em Mecânica Clássica. Em vez de trajetória, o movimento de partículas em Mecânica Quântica é descrito por meio de uma função de onda, que é uma função da posição da partícula e do tempo. A função de onda é interpretada por Max Born como uma medida da probabilidade de se encontrar a partícula em determinada posição e em determinado tempo. Esta interpretação é a mais aceita pelos físicos hoje, no conjunto de atribuições da Mecânica Quântica regulamentados pela Escola de Copenhagen. Para descrever a dinâmica de um sistema quântico deve-se, portanto, achar sua função de onda, e para este efeito usam-se as equações de movimento, propostas por Werner Heisenberg e Erwin Schrödinger independentemente.
Apesar de ter sua estrutura formal basicamente pronta desde a década de 1930, a interpretação da Mecânica Quântica foi objeto de estudos por várias décadas. O principal é o problema da medição em Mecânica Quântica e sua relação com a não-localidade e causalidade. Já em 1935, Einstein, Podolski e Rosen publicaram seu Gedankenexperiment, mostrando uma aparente contradição entre localidade e o processo de Medida em Mecânica Quântica. Nos anos 60 J. S. Bell publicou uma série de relações que seriam respeitadas caso a localidade — ou pelo menos como a entendemos classicamente — ainda persistisse em sistemas quânticos. Tais condições são chamadas desigualdades de Bell e foram testadas experimentalmente por A. Aspect, P. Grangier, J. Dalibard em favor da Mecânica Quântica. Como seria de se esperar, tal interpretação ainda causa desconforto entre vários físicos, mas a grande parte da comunidade aceita que estados correlacionados podem violar causalidade desta forma.
Tal revisão radical do nosso conceito de realidade foi fundamentada em explicações teóricas brilhantes para resultados experimentais que não podiam ser descritos pela teoria clássica, e que incluem:
- Espectro de Radiação do Corpo negro, resolvido por Max Planck com a proposição da quantização da energia.
- Explicação do experimento da dupla fenda, no qual eléctrons produzem um padrão de interferência condizente com o comportamento ondular.
- Explicação por Albert Einstein do efeito fotoelétrico descoberto por Heinrich Rudolf Hertz, onde propõe que a luz também se propaga em quanta (pacotes de energia definida), os chamados fótons.
- O Efeito Compton, no qual se propõe que os fótons podem se comportar como partículas, quando sua energia for grande o bastante.
- A questão do calor específico de sólidos sob baixas temperaturas, cuja discrepância foi explicada pelas teorias de Einstein e de Debye, baseadas na equipartição de energia segundo a interpretação quantizada de Planck.
- A absorção ressonante e discreta de energia por gases, provada no experimento de Franck-Hertz quando submetidos a certos valores de diferença de potencial elétrico.
- A explicação da estabilidade atômica e da natureza discreta das raias espectrais, graças ao modelo do átomo de Bohr, que postulava a quantização dos níveis de energia do átomo.
O desenvolvimento formal da teoria foi obra de esforços conjuntos de muitos físicos e matemáticos da época como Erwin Schrödinger, Werner Heisenberg, Einstein, P.A.M. Dirac, Niels Bohr e John von Neumann, entre outros (de uma longa lista).
Formalismos na mecânica quântica
Mais tarde, foi introduzido o formalismo hamiltoniano, baseado matematicamente no uso do lagrangiano, mas cuja elaboração matemática é muitas vezes mais fácil.
_________________________________________________________
__________________________________
 | ||||||||||||||||
| Princípio da Incerteza | ||||||||||||||||
Introducão a...
|








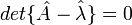

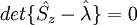








0 comentários:
Postar um comentário